機率密度函式 (Probability Density Function)
機率密度函式的要求 (Requirements for a Probability Density Function)
1. f(x) >= 0 for all x between a and b
2. f(x)曲線在 a 和 b 之間的總面積 = 1.0
其中 f(x) 為一機率密度函式,其定義域為 a<=x<=b對於連續型隨機變數,在單一點發生的機率是0,因此只能估計在一區間內的機率,而在一區間內的機率,就是機率密度函式在該區間內的面積。
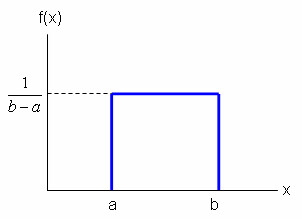
均勻分佈 (Uniform Distribution)
均勻機率密度函式 (Uniform Probability Density Function)
\( f(x) = \frac{1}{b-a} \)
其中 \( a \leq x \leq b\)
常態分佈 (Normal Distribution)
常態機率密度函式 (Normal Density Function)
\( f(x) = \frac{1}{\sigma \sqrt{2 \pi}}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \)
其中
\( \mu \): 平均值 (mean)
\( \sigma \): 標準差 (standard deviation)
\( \sigma^2 \): 變異數 (variance)
\(-\infty \lt x \lt \infty \)
\( e = 2.71828... \)
\( \pi = 3.14159... \)
Excel 函數
若要計算累積常態機率(cumulative normal probabilities) P(X<x),Excel 函數為 NORMDIST(x, μ, σ, True)。
其中 True 代表要計算 cumulative normal probability, False 代表要計算 normal density function。若要計算x,使得 P(X<x) = A,Excel 函數為 NORMINV(A, μ, σ)。
舉例,一投資標的之報酬率為常態分佈,平均值為10%,標準差為5%。
賠錢的機率為
\( P(X<0) = P(\frac{X-\mu}{\sigma} \lt \frac{0-10\%}{5\%}) = P(Z<-2) = 0.0228 \)
其中Z為標準常態隨機變數(standard normal random variable, μ=0, σ=1)。
延伸閱讀
[書籍] Managerial Statistics, Chap 8 Continuous Probability Distributions, 作者: Gerald Keller
[WiKi] Normal distribution